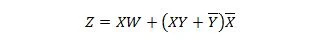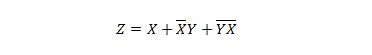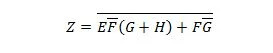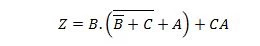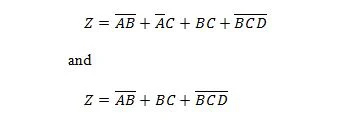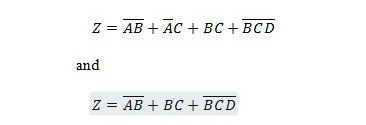2. peatükk: Boole'i algebra ja sellega seotud arvutikomponendid
2.1 Põhilised Boole'i operaatorid
Oletame, et mina (autor) olen pikk ja sina (lugeja) oled pikk. Kui keegi küsib, kas me mõlemad oleme pikad, vastaksite 'Jah' (tõsi). Kui ta küsib, kas me mõlemad oleme lühikesed, vastaksite 'Ei' (vale). Kui sa oled lühike ja mina pikk ning ta küsib sinult, kas sina või mina oleme pikk, oleks sinu vastus „Jah” (tõsi). Kui ta küsib, kas sina ja mina oleme pikad, ei oleks teil vastust. Võite jätkata, et viimast küsimust ei tohiks esitada või et küsimusele ei ole vastust. Noh, ma tahan, et te (lugeja) teaksite, et täna tuleks teatud asjaoludel see küsimus esitada.
Bioloogias on inimene kas pikk või lühike. Just “keskkonna” tingimused muudavad inimese keskmise pikkusega. Üks teadlane George Boole määratles seda tüüpi küsimuste jaoks vastused või reeglid. Õpime neid reegleid veebipõhise karjäärikursuse selles osas (peatükk). Neid reegleid kasutatakse tänapäeval andmetöötluses, programmeerimises, elektroonikas ja telekommunikatsioonis. Tegelikult poleks teil ilma nende reegliteta arvutit, nagu see tänapäeval tavaline; sul ei oleks ka programmeerimist, nagu see tänapäeval on tavaline.
Õige või vale
Lihtne inimkeelne väide on iseenesest kas tõene või väär. Kui ma ütlen: 'Ma olen pikk', on see kas tõsi või vale. Kui ma ütlen: 'Sa oled pikk', on see kas tõsi või vale. Kui mina olen pikk ja sina lühike ja küsitakse, kas nii sina kui mina oleme pikad, tuleb Boole'i loogikas vastata kas tõene või vale. Milline neist kahest tuleks anda? Boole sellele küsimusele tegelikult ei vastanud. Ta lihtsalt mõtles välja reeglid, mida järgida. Hea uudis on see, et kui järgite neid reegleid nende õiges kontekstis, ei teki teil ebaselgust. Tänu nendele reeglitele on meil tänapäeval arvutid ja programmeerimine. Reeglid on teile nüüd antud. Reegleid ei saa tegelikult seletada; sa lihtsalt aktsepteerid neid. Reeglid on kolme pealkirja all: JA, VÕI ja EI.
JA
Küsimuse võib esitada, kui nii sina kui mina oleme pikad. Minu pikkus ja teie pikkus kombineeritakse siis JA reeglitega. Järgida tuleb järgmisi JA-reegleid:
vale JA vale = vale
vale JA tõene = vale
tõene JA vale = vale
tõsi JA tõsi = tõsi
Nüüd olgu pikk tõsi ja lühike vale. See tähendab, et kui mina olen lühike JA sina oled lühike, siis sina ja mina oleme lühikesed. Kui mina olen lühike JA sina oled pikk, siis sina ja mina oleme lühikesed; see on Boole'i vastus, millega peate nõustuma. Kui mina olen pikk JA sina oled lühike, siis nii sina kui mina oleme lühikesed. Kui mina olen pikk JA sina oled pikk, siis sina ja mina oleme pikad. Kõik need on JA Boole'i reeglid, millega teie (lugeja) peate lihtsalt nõustuma.
VÕI
Võib küsida, kas sina VÕI mina oled pikk. Minu pikkus ja teie pikkus kombineeritakse seejärel VÕI reeglistikuga. Järgida tuleb järgmisi VÕI-reegleid:
vale VÕI vale = vale
vale VÕI tõene = tõsi
tõene VÕI vale = tõsi
tõsi VÕI tõsi = tõsi
Jällegi olgu pikk tõsi ja lühike vale. See tähendab, et kui mina olen lühike VÕI sina oled lühike, siis sina VÕI mina olen lühike. Kui mina olen lühike VÕI sina pikk, oled sina või mina pikk. Kui mina olen pikk VÕI sa oled lühike, siis sina VÕI mina on pikk. Kui mina olen pikk VÕI sina oled pikk, oled sina või mina pikk. Kõik need on Boole'i reeglid, millega peate nõustuma.
MITTE
Nüüd on Boole'i loogikas ainult kaks olekut (võimalikud vastused). See tähendab, et kui sa EI ole pikk, oled sa lühike. Kui sa EI OLE lühike, siis oled pikk; mitte midagi muud. Need on EI reeglid, mida järgida:
EI ole vale = tõsi
EI ole tõsi = vale
Oletame, et teil on nöör (või vedru), mida saate pikendada (tõmmata). Kui string on oma loomulikus olekus, siis kui ma ütlen 'MITTE lühike', pikendaksite seda; see on tõlgendus. Kui stringi pikendatakse, siis kui ma ütlen 'MITTE pikk', lubaksite sellel kokku tõmbuda; see on tõlgendus.
Peate pähe õppima kõik antud reeglid nende erinevates kategooriates.
Rohkem kui kaks operandi
Arvutikeeles nimetatakse nii AND, OR ja NOT operaatoriks. Operaatori NOT jaoks on vastuse saamiseks vaja ainult ühte operandit (väärtus operaatorile). Operaatorite JA või VÕI puhul võib teil olla rohkem kui kaks operandi. Eelmised juhtumid näitavad kahte operandi JA ja VÕI. AND jaoks võib olla kolm operandi järgmiselt:
vale JA vale JA vale = vale
vale JA vale JA tõene = väär
Need on kaks rida; mõlemal on kaks JA-operaatorit. Kui operandid on kolm, on tegelikult üheksa rida. Operaatori AND korral võrdub ainult viimane rida (üheksas rida) tõega; kõik eelnevad read on valed. Pange tähele, et kahe operandi AND korral on ainult viimane rida tõene still; kõik kolm eelnevat rida on valed. Kui operandid on neli, on rida 16 ja ainult viimane rida kehtib AND-operaatori puhul.
AND muster ja OR muster on erinevad. Kahe VÕI-operandi kolme operandiga on samuti üheksa rida ja ainult esimene rida on seekord vale. Teine kuni üheksanda rida on tõsi. Pange tähele, et kahe operandi VÕI puhul on ainult esimene rida tõene; kõik ülejäänud kolm rida on valed. Kui VÕI operandid on neli, on ka 16 rida.
Operaator NOT tegeleb ainult ühe operandiga. EI ole vale on tõene ja EI ole tõene on vale.
2.2 Kahe operandi tõetabel ja nende elektroonilised komponendid
Matemaatikas on teema, mida nimetatakse algebraks. Väike osa sellest oli näha eelmises peatükis. On olemas algebra, mida nimetatakse Boole'i algebraks. Boole'i algebras tuvastatakse tõene kahe põhinumbri järgi, mis on 1, ja väära kahe põhikoha järgi, mis on 0.
Arvuti sisemised komponendid on elektroonilised komponendid. Arvutisüsteemi süsteemiüksusel on digitaalsed elektroonilised komponendid. JA-operatsiooni teeb väike elektrooniline komponent, mida nimetatakse JA-väravaks. VÕI-toimingut teostab väike elektrooniline komponent, mida nimetatakse VÕI-väravaks. EI-operatsiooni teeb väike elektrooniline komponent, mida nimetatakse EI-väravaks. Liiga palju neid väravaid võib olla integraallülituse (IC) kiibis.
JA Tõelaud ja selle värav
Järgmises tabelis on toodud AND tõetabel ning selle JA värava (väikering) sümbol:
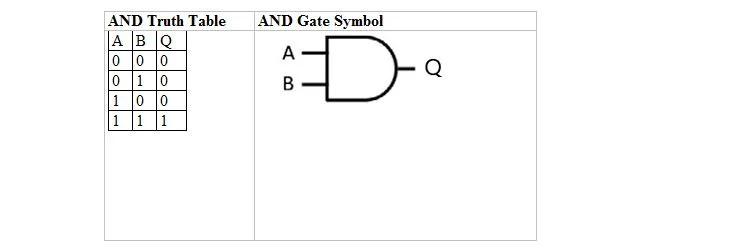
Nii tõetabeli JA kui ka selle värava jaoks on A ja B kaks sisendmuutujat. Q on väljundmuutuja. A on kas 1 või 0. B on kas 1 või 0. Q on kas 1 või 0. JA tõesuse tabel 1 ja 0-ga on sama, mis eelmine tõene/väär JA tõe paigutus (tabel). Võrrand JA on:
A . B = Q
kus punkt (.) tähendab JA (tõuväärtus). Punkti võib ära jätta, kui AB = Q, mis tähendab sama asja (JA).
Märkus. Neljas reas olevad bitid A ja B jaoks on paaridena esimesed neli numbrit teises aluses, mis algavad 0-st (või 00-st), st 00, 01, 10, 11.
Järgmises tabelis on toodud VÕI tõesuse tabel ja selle VÕI värava (väikering) sümbol:
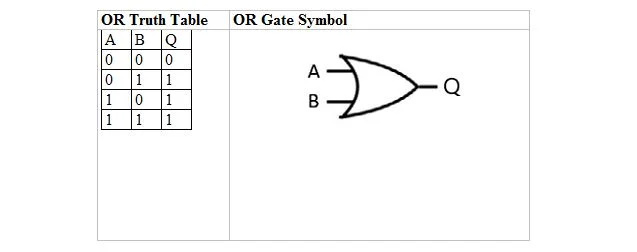
Nii VÕI tõetabeli kui ka selle värava jaoks on A ja B kaks sisendmuutujat. Q on väljundmuutuja. VÕI tõetabel 1-de ja 0-dega on sama, mis eelmine tõene/väär VÕI tõe paigutus (tabel).
VÕI võrrand on järgmine:
A + B = Q
Kus + tähendab siin Boole'i VÕI, mitte liitmist. Võrrand loetakse kui 'A või B võrdub Q'.
Järgmises tabelis on toodud EI-tõe tabel ja selle EI-värava (väikeahela) sümbol:
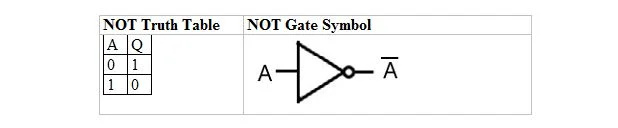
NOT tõesuse tabelil või NOT väraval on ainult üks sisend ja üks väljund. Kui sisend on 0, on väljund 1. Kui sisend on 1, on väljund 0. NOT värav teeb omamoodi inversiooni. Väljundmuutuja on sama, mis sisendmuutujal, kuid ribaga (üle joonitud). EI-tõetabel 1-de ja 0-dega on sama, mis eelmine tõene/väär VÕI tõe paigutus (tabel).
Võrrand EI on järgmine:
A = Q
Kus Q = A ja riba A kohal tähendab siin täiendit. 0 täiendus on 1 ja 1 täiendus on 0. EI-värav on tuntud ka kui INVERTING värav.
Need on põhitõe (või juur) tabelid ja nende väravad (väikesed vooluringid) digitaalelektroonikas (koos Boole'i algebraga). Ülejäänud kolm tõesuse tabelit, mis on toodud järgmisel joonisel, ja nende väravad on mugavuse huvides ja põhinevad kolmel eelmisel tõetabelil.
On tõetabel ja värav, mis on tuletatud JA tõe tabelist ja väravast. Neid nimetatakse NAND (for NOT AND) tõetabeliks ja vastavaks NAND-väravaks. NAND-i tõetabel ja selle NAND-värav on:
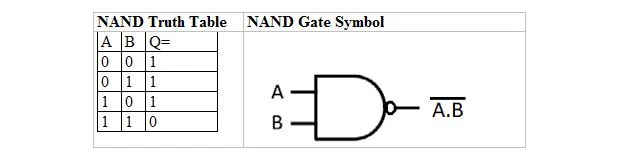
NAND-tõelisuse tabeli saamiseks minge AND tõesuse tabeli väljundisse ja asendage iga number selle täiendiga. 0 täiendus on 1 ja 1 täiend on 0. NAND-värav on nagu JA-värav, kuid sellel on väljundrea ees väike ring. NAND-i võrrand on järgmine:
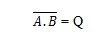
Kus tähendab 'A' JA 'B' tulemuse täiendit. Riba (ülejoon) on väravas kujutatud väikese ringiga. Pange tähele, et punkti A ja B vahel võib ära jätta.
On veel üks tõetabel ja värav, mis on tuletatud VÕI tõetabelist ja väravast. Neid nimetatakse NOR (for NOT OR) tõetabeliks ja vastavaks NOR-väravaks. NOR-tõe tabel ja selle NOR-värav on:
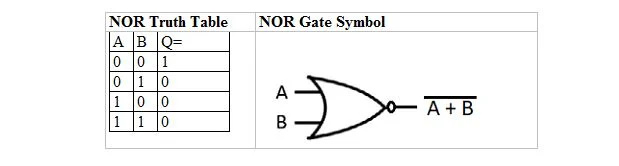
VÕI tõesuse tabeli saamiseks minge VÕI tõesuse tabeli väljundisse ja asendage iga number selle täiendiga. 0 täiend on 1 ja 1 täiend on 0. NOR-värav on nagu VÕI-värav, kuid sellel on väljundrea ees väike ring. Võrrand NOR on:
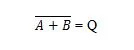
Kus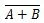 
tähendab 'A' VÕI 'B' tulemuse täiendit. Riba (ülejoon) on väravas kujutatud väikese ringiga.
Eksklusiivne VÕI (XOR)
VÕI-värava tõetabel on järgmine:
Tavalises inglise keeles pole selge, kas 1 VÕI 1 viimane rida peaks andma 1 või 0. Seega on Boole'i algebras kahte tüüpi VÕI tõetabeleid ja kaks vastavat väravat. Tavalise VÕI puhul annab 1 VÕI 1 viimane rida 1. Teist tüüpi VÕI on välistav VÕI (XOR), kus esimesed kolm rida on samad, mis tavalise VÕI kolm esimest rida (kaasa arvatud väljund). Neljanda ja viimase rea puhul annab 1 VÕI 1 aga 0.
Järgmises tabelis on toodud XOR-i tõesuse tabel ja selle XOR-värava (väikese vooluringi) sümbol:
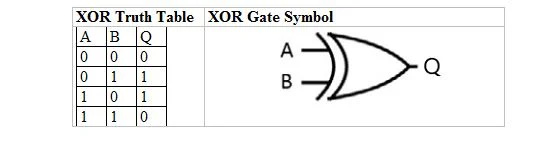
Nii XOR-i tõetabeli kui ka selle värava jaoks on “A” ja “B” kaks sisendmuutujat. 'Q' on väljundmuutuja.
XOR võrrand on järgmine:
A ⊕ B = Q
Kus ⊕ tähendab siin Boole'i XOR-i.
Tavaline VÕI tähendab üht või mõlemat. Eksklusiivne VÕI tähendab rangelt kas ja mitte mõlemat.
2.3 Boole'i postulaadid
Postulaadid on oletused, mille põhjal tehakse teatud järeldused. Seal on kümme Boole'i postulaati, mis on juurdunud võrranditest JA, VÕI ja EI (tõetabelid). Neid võrrandeid nimetatakse ka funktsioonideks. Põhifunktsioonid kopeeritakse järgmiselt:
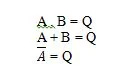
Need on Boole'i algebra põhifunktsioonid (võrrandid). Järgmised kolm ülejäänud (funktsioonide) võrrandit ei ole põhifunktsioonid:
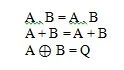
Kuigi viimane funktsioon on siin omapärane, ei peeta seda põhifunktsiooniks.
Boole'i postulaadid on järgmised:
Funktsioonist JA
1) 0. 0 = 0
kakskümmend . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Funktsioonist VÕI
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Funktsioonist NOT Function
9) 0 = 1
10) 1 = 0
Märge: Need postulaadid on ainult read AND-, OR- ja NOT-tõdetabelites, mida väljendatakse sõltumatul viisil. Lugeja peaks etteantud postulaadid pähe õppima.
2.4 Boole'i omadused
Omadus on nagu millegi omadus. Boole'i omadused on võrrandid, mis on tuletatud Boole'i postulaatidest. Selles jaotises antakse omadused lihtsalt ilma nende tuletusteta ja seejärel kasutatakse neid hiljem. Kakskümmend viis atribuuti on rühmitatud kümne pealkirja alla järgmiselt:
Funktsiooni JA omadused
Atribuut 1:
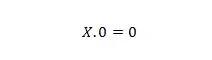
Kus X võib olla 1 või 0. See tähendab, et olenemata sellest, mis X on, on tulemus alati 0.
Märkus. Muutuja ei pea tingimata olema A või B, C või D. Muutuja võib olla W või X või Y või Z või mis tahes muu täht.
Atribuut 2:
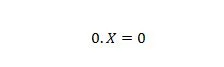
Kus X võib olla 1 või 0. Pange tähele, et omaduse 1 ja omaduse 2 erinevus seisneb selles, et mõlema võrrandi võrdusmärgi vasakul poolel on X ja 0 positsioonid vahetatud.
Atribuut 3:
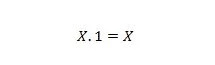
Kui X on 0, siis 0. 1 = 0. Kui X on 1, siis 1. 1 = 1.
Atribuut 4:
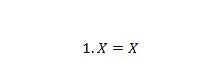
Kui X on 0, siis 1. 0 = 0. Kui X on 1, siis 1. 1 = 1. Pange tähele, et omaduse 3 ja omaduse 4 erinevus seisneb selles, et mõlema võrrandi vasakul küljel on X ja 1 on vahetatud.
Funktsiooni VÕI omadused
Atribuut 5:
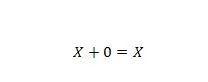
Kus X võib olla 1 või 0. See tähendab, et kui X on 0, on tulemus 0. Kui X on 1, on tulemus 1.
Atribuut 6:
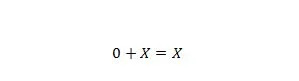
Kus X võib olla 1 või 0. Pange tähele, et omaduse 5 ja omaduse 6 erinevus seisneb selles, et mõlema võrrandi vasakus servas on X ja 0 positsioonid vahetatud.
Atribuut 7:
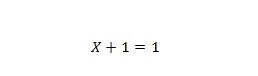
Kui X on 0, siis 0 + 1 = 1. Kui X on 1, siis 1 + 1 = 1.
Atribuut 8:
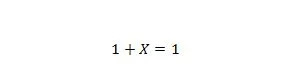
Kui X on 0, siis 1 + 0 = 1. Kui X on 1, siis 1 + 1 = 1. Pange tähele, et atribuutide 7 ja 8 erinevus seisneb selles, et mõlema võrrandi vasakul küljel on X ja 1 on vahetatud.
Omadused muutuja enda või selle täiendusega kombineerimise kohta
Atribuut 9: 
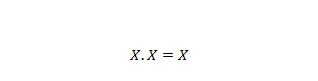
See tähendab: kui X on 0, siis 0 . 0 = 0. Kui X on 1, siis 1 . 1 = 1.
Atribuut 10:
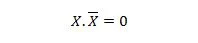
See tähendab: kui X on 0, siis 0. 1 = 0. Kui X on 1, siis 1. 0 = 0.
Järjestikuste muutujate puhul muutub see omadus:
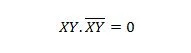
Atribuut 11:
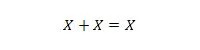
See tähendab: kui X on 0, siis 0 + 0 = 0. Kui X on 1, siis 1 + 1 = 1 (tavalisest VÕI).
Atribuut 12:
See tähendab: kui X on 0, siis 0 + 1 = 1. Kui X = 1, siis 1 + 0 = 1.
See tähendab: kui X on 0, siis 0 + 1 = 1. Kui X = 1, siis 1 + 0 = 1.
Kahekordne täiendamine
Atribuut 13:
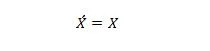
Kui X vasakpoolses servas on 0, muutub X paremal küljel 0. Kui X paremal küljel on 1, muutub vasakpoolne X väärtuseks 1. Teisisõnu, topelttäiendid annavad tagasi algse väärtuse.
Kommutatiivne seadus
Atribuut 14:
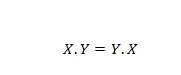
See tähendab, et esimese ja teise operandi vahetamine AND-operaatori jaoks võrdusmärgi vasakul küljel ei oma tähtsust; vastus on ikka sama, kui vasakpoolne vahetus on toimunud. Selle võrrandi saab kirjutada punktide väljajätmisega järgmiselt: XY = YX.
Atribuut 15:
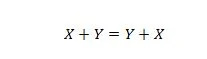
Siin on seletus sama, mis eelmises JA, kuid see on operaatori VÕI jaoks.
Jaotusseadus
Atribuut 16:
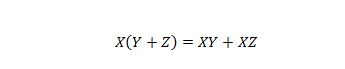
Siin on kolm muutujat: X, Y ja Z. Iga muutuja võib olla kas 1 või 0. Võrdsussümboli vasakpoolses servas tähendavad sulud kõigepealt selles sisalduva hindamist. Siis JA on tulemuseks X. Parempoolne külg ütleb, et X JA Y koos VÕI X JA Z koos on samad, mis vasak pool. Pange tähele, et AND-ide punktioperaator on täielikult välja jäetud; ja ühendatud muutujad tähendavad ikkagi JA.
Atribuut 17:
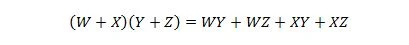
See omadus on atribuudi 16 laiendus, millele on lisatud muutuja W.
Assotsiatiivne seadus
Atribuut 18:
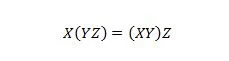
Sulgudes tuleb kõigepealt hinnata, mis sulgudes on. Seega, kui vasakpoolses avaldises on Y koos Z-ga kõigepealt JA ja X on tulemusega AND, siis see vasakpoolne lõpptulemus on sama, mis parempoolne lõpptulemus -käepool, kus X koos Y-ga on AND-i enne AND-jaotmist tulemusega Z-ga. Pange tähele, et võrrandis on punktid välja jäetud.
Atribuut 19:
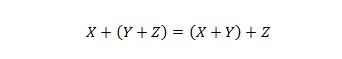
Seda omadust selgitatakse sarnaselt atribuudiga 18, kuid operaatori AND asemel kasutatakse operaatorit VÕI. VÕI-operaatorit + ei jäeta kunagi Boole'i avaldisest lihtsuse huvides välja. Teisest küljest võib AND-operaatori ära jätta ja kaks muutujat ühendada.
Imendumine
Atribuut 20:
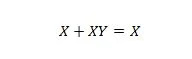
Selle võrrandi korral on parem pool alati X (absorbeeritud), olenemata sellest, mis Y on.
Atribuut 21:
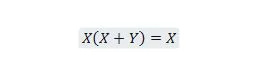
Samuti on selle võrrandi korral parem pool alati X (neeldunud), olenemata sellest, mis Y on. See omadus 21 on sama, mis atribuut 20, mis on:
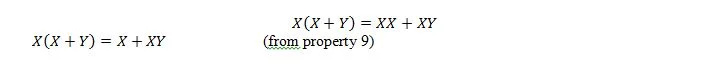
Siin kasutame jaotusseadust ja asjaolu, et X.X = X omadusest 9.
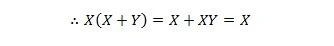
Identiteet
Atribuut 22:
See tähendab, et X + Y avaldise puhul X-i komplement Y ees ei muuda avaldist.
Atribuut 23:
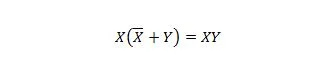
See tähendab, et XY-avaldise puhul ei muuda XY-avaldist X ORed koos sulgudes oleva Y-ga, mis tehakse esimesena.
DeMorgani seadus
Atribuut 24:
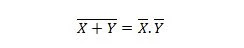
See tähendab, et VÕI (EI VÕI) väraval on sama tulemus kui kahe sisendi MÄRKAMISEKS enne AND-i märkimist.
Atribuut 25:
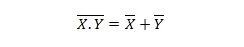
See tähendab, et NAND (NOT AND) väraval on sama tulemus kui kahe sisendi MÄRKAMISEKS enne VÕI-d.
Pakutud illustratsioonid on 25 atribuuti. Neid saab tõestada, asendades kõik erinevad võimalikud 1-de ja 0-de väärtused igas vasakpoolses avaldises, et näha, kas parempoolne avaldis (või tulemus) saadakse. Tõestused on jäetud lugejale harjutuseks.
2.5 Liitväljendite lihtsustamine
Järgmised kaks funktsiooni on samad:
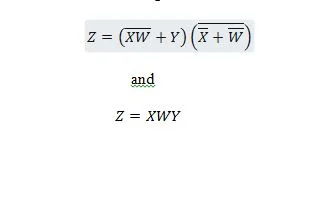
Z on väljund ning X, W ja Y on sisendid. Esimene vajab NAND-väravat, VÕI-väravat, JA-väravat, kahte MITTE-väravat, VÕI-väravat ja NOR-väravat. Teine vajab ainult kahte JA väravat. Esimene on võrrand, millel on parempoolne liitavaldis, mis on teise võrrandi jaoks lihtsustatud (taandatud) ühe parempoolse avaldise liikmeks.
Lihtsustamine või vähendamine toob kaasa vähem väravate arvu, et rakendada sama funktsiooni kui vooluringi. Selline väiksem vooluahel võib olla integraallülituse (IC) osa või iseseisev vooluahel arvuti emaplaadi pinnal.
Kui funktsioon (võrrand) saabub projekteerimisprotsessi, tuleb väravate arvu vähendamiseks ja odavama vooluringi saamiseks läbi viia lihtsustamine. Lihtsustamine nõuab ühe või enama eelmisest kahekümne viiest Boole'i atribuudist.
Näide 2.51:
Vähendage võrrandit:
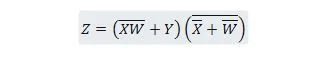
Märge: Kaks kõrvuti olevat sulgu tähendab, et sulgud on JA-ga (nende vahele jäävat punkti pole valikuliselt kirjutatud).
Lahendus:
Lahenduste puhul on iga sammu põhjendus (põhjus) toodud sammust paremal, sulgudes. Lugeja peaks lugema iga sammu ja selle põhjendust. Lugeja peaks funktsiooni vähendamise etappe lugedes viitama ka eelmistele omadustele.
Näide 2.52:
Lihtsustama:
2.6 Minimaalne toodete summa
Järgmised kaks funktsiooni on samad:
Mõlema võrrandi mõlemad parempoolsed avaldised on väidetavalt toodete summa (SP) kujul. Ekspressavaldis öeldakse olevat tootesumma kujul, kui sellel ei ole sulgusid. On ilmne, et esimene funktsioon (võrrand) vajab rohkem väravaid kui teine funktsioon.
Esimest parempoolset väljendit saab teise funktsiooni saamiseks siiski vähendada. Teist parempoolset avaldist ei saa enam lihtsustada ja seda võib siiski väljendada toodete summana (terminite lisamine). Teist parempoolset väljendit ei saa tegelikult enam lihtsustada. Niisiis, väidetavalt on see toodete minimaalse summa (MSP) kujul.
Näide 2.61:
Viige järgmine funktsioon esmalt vormile Toodete summa ja seejärel vormile Minimaalne toodete summa.
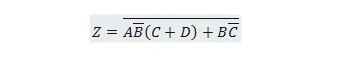
Lahendus:
Selliste probleemide lahendamisel tuleb kasutada ühte või mitut eelmisest kahekümne viiest omadusest, nagu on näidatud selles lahenduses:
2.6 Minimaalne toodete summa
Järgmised kaks funktsiooni on samad:
Mõlema võrrandi mõlemad parempoolsed avaldised on väidetavalt toodete summa (SP) kujul. Ekspressavaldis öeldakse olevat tootesumma kujul, kui sellel ei ole sulgusid. On ilmne, et esimene funktsioon (võrrand) vajab rohkem väravaid kui teine funktsioon.
Esimest parempoolset väljendit saab teise funktsiooni saamiseks siiski vähendada. Teist parempoolset avaldist ei saa enam lihtsustada ja seda võib siiski väljendada toodete summana (terminite lisamine). Teist parempoolset väljendit ei saa tegelikult enam lihtsustada. Niisiis, väidetavalt on see toodete minimaalse summa (MSP) kujul.
Näide 2.61:
Viige järgmine funktsioon esmalt vormile Toodete summa ja seejärel vormile Minimaalne toodete summa.
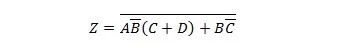
Lahendus:
Selliste probleemide lahendamisel tuleb kasutada ühte või mitut eelmisest kahekümne viiest omadusest, nagu on näidatud selles lahenduses:
See viimane avaldis on toodete summa kujul (SP), kuid mitte toodete minimaalse summa kujul (MSP). Küsimuse esimene osa on vastatud. Teise osa lahendus on järgmine:
See viimane lihtsustatud funktsioon (võrrand) on MSP-vormingus ja vajab rakendamiseks vähem väravaid kui sellele vastav SP-vorm. Pidage meeles: SP tähendab toodete summat, samas kui MSP tähendab toodete minimaalset summat.
Näide 2.62:
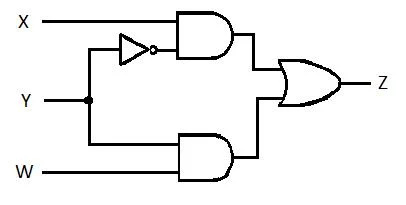
Järgmisel vooluringil on X-, Y- ja W-sisendid ning Z on väljund. Looge Z jaoks funktsioon Toodete summa (SP) (nähtav minimaalse toodete summa funktsioon). Seejärel looge tegelik rohkem vähendatud (minimeeritud) toodete summa (MSP). Seejärel rakendage MSP-ahel (joonistage MSP-väravavõrk).
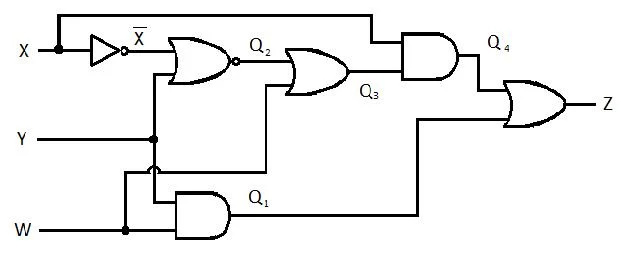
Joonis 2.61 A piiramisahel
Lahendus:
Enne lihtsustamisprotsessi algust tuleb Z avaldis hankida X, Y ja W kujul. Vaadake seda diagrammi illustratsiooni näidet:
See on Z avaldis X, Y ja W kaudu. Pärast seda võib toimuda lihtsustamine näiliseks MSP-ks. Ilmselt MSP on SP.
See viimane võrrand (funktsioon) on SP kujul. See ei vasta tõele. Toodete miinimumsumma (veel mitte MSP). Seega peab vähendamine (minimeerimine) jätkuma.
See viimane võrrand (funktsioon) on tõeline toodete minimaalne summa (MSP). Ja toodete minimaalne summa (tõeline minimeerimine) väravaahel on:
Joonis 2.62 MSP väravaahel
kommenteerida
Selle jaotise analüüsist on näha, et pole selge, kas toodete summa on toodete minimaalne summa või mitte. SP pole eriti kasulik. Just MSP on väga kasulik. MSP saamiseks on kindel viis; selleks on kasutada Karnaugh kaarti. Karnaugh Map ei kuulu selle veebipõhise karjäärikursuse ulatusse.
2.7 Probleemid
Lugejal soovitatakse enne järgmise peatüki juurde liikumist lahendada kõik peatüki ülesanded.
- Koostage AND, OR ja NOT tõesuse tabelid koos nende vastavate väravatega.
- Kirjutage kümme Boole'i postulaati nende erinevatesse kategooriatesse ja nimetage kategooriad.
- Kirjutage ilma selgituseta Boole'i algebra kakskümmend kuus omadust erinevatesse kategooriatesse, nimetades kategooriad.
- Vähendage võrrandit kasutades Boole'i omadusi ja tsiteerides kasutatud kategooriaid.
- Vähendage võrrandit kasutades Boole'i omadusi ja tsiteerides kasutatud kategooriaid.
- Kasutades Boole'i atribuute ja tsiteerides kasutatud kategooriaid, redigeerige järgmine võrrand – esmalt toodete summaks ja seejärel toodete minimaalseks summaks:
- Kasutades Boole'i atribuute ja tsiteerides kasutatud kategooriaid, redigeerige järgmine võrrand – esmalt toodete summaks ja seejärel toodete minimaalseks summaks:
